

What is the set D and write out the predicate function P(n) in symbolic form? This should be as simple as possible. This will be expressed symbolically as a conjecture of the form VnED, P(n). b) In Q2, you will be proving that the second algorithm is never more expensive than the first. Do not forget to state for which values of n the recurrence relation applies. The Tower of Hanoi (also called The problem of Benares Temple or Tower of Brahma or Lucas' Tower and sometimes pluralized as Towers, or simply pyramid puzzle) is a mathematical game or puzzle consisting of three rods and a number of disks of various diameters. Tower of Hanoi interactive display at Mexico City's Universum Museum. Your definition needs initial condition(s) and the recurrence relation. An animated solution of the Tower of Hanoi puzzle for T(4, 3). AP EAMCET E & AM (Engineering, Agriculture & Medical) Study Guide. Illustrates the natural relationship between. For large enough values of n, H(n) is a function of H(n-2). Interactive video lesson plan for: Towers of Hanoi Induction Proof Activity overview: Example of a proof by induction: The number of steps to solve a Towers of Hanoi problem of size n is (2n) -1. A2-Part 1.docx A2-Part 1.pdfĪ) (2 marks) Give the recursive definition of H(n), which is the cost of moving n disks in the second algorithm. The files below have also been chopped up into two separate pages which are available separately in the two Crowdmark questions. At the top level, we will want to move the entire tower, so we want to move disks 5 and smaller from peg A to peg B. The rest of this assignment is described in the two-page handout underneath, which you can edit, and then upload page by page into the appropriate Crowdmark questions. Our function will also take three parameters indicating from which peg the tower should be moved (source), to which peg it should go (dest), and the other peg, which we can use temporarily to make this happen (spare). The second algorithm recursed on n-2 disks and its cost was also described by a recursive sequence H(n), that you had to describe in the assignment Solutions will be posted on February 17 and you can verify at that time that you are working with the correct function. The first algorithm recursed on n-1 disks and its cost was described by the recursively defined sequence: o T(1) = 1 T(K) = 4T(k-1) + 1 for k> 1 2. The unit cost of these algorithms was the cost of transferring one single disk to the next pole in clockwise fashion.
Hanoi towers big oh proof by induction how to#
Each algorithm described how to transfer n disks from one pole to the next. Hanoi puzzle is a classical divide et conquer problem. Well discover two powerful methods of defining objects, proving concepts, and implementing programs recursion and induction. Basic programming knowledge is necessary as some quizzes require programming in Python.Transcribed image text: In Part 1 of the assignment you will compare the cost of two recursive circular Tower of Hanoi algorithms that you were asked to develop in Question 1 of Assignment 1. According to the literature as we can see in the proof, the Towers of. Big O notation is the most used notation to express the time complexity of an algorithm. Video created by for the course 'Mathematical Thinking in Computer Science'.
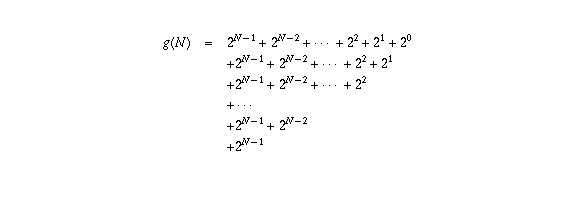
Well discover two powerful methods of defining objects, proving concepts, and implementing programs recursion. We assume only basic math (e.g., we expect you to know what is a square or how to add fractions), common sense and curiosity.Ģ. Video created by Universidade da Califórnia, San Diego, Universidade HSE for the course 'Mathematical Thinking in Computer Science'. In the online course, we use a try-this-before-we-explain-everything approach: you will be solving many interactive (and mobile friendly) puzzles that were carefully designed to allow you to invent many of the important ideas and concepts yourself.ġ. We will use these tools to answer typical programming questions like: How can we be certain a solution exists? Am I sure my program computes the optimal answer? Do each of these objects meet the given requirements? In this course, we will learn the most important tools used in discrete mathematics: induction, recursion, logic, invariants, examples, optimality.

Mathematical thinking is crucial in all areas of computer science: algorithms, bioinformatics, computer graphics, data science, machine learning, etc.


 0 kommentar(er)
0 kommentar(er)
